Java Fundamentals

Summary of the last lecture

• We learnt to use eclipse to write and run java code
• We began to see the control flow statement through the if(){}else{} and switch(){case:} statements

Program execution flow : Activity Diagram

• The activity diagram is very less difficult to write than a class diagram
• The activity diagram can often be confused with the state diagram, which we will see just after
• The activity diagram can naturally be written from the natural language expression of the algorithm

Program execution flow : Activity Diagram (2)

Program execution flow : Activity Diagram (4)

• Activity symbolizes an operation in the algorithm
  
• Gate symbolizes a decision point or a join in the treatment
  

Program execution flow: Activity Diagram (5)

• Fork Symbolizes several operations run in parallel
  

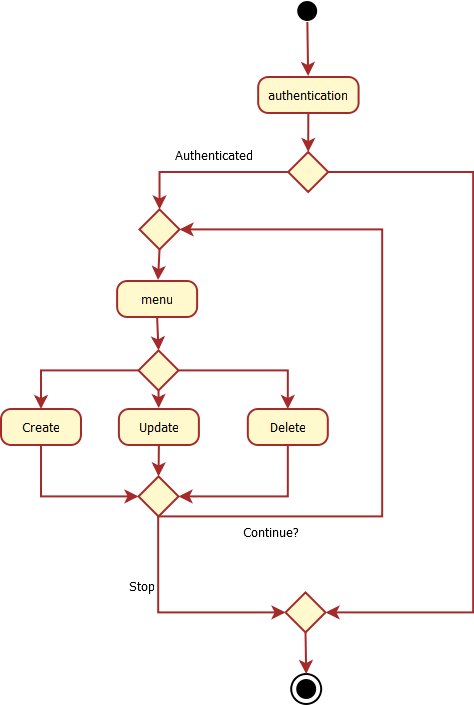
Exercise (part of the project) : Realize the authentication of the application

• This corresponds to the first part of the activity diagram
• The good "credentials" (couple of a login and a password) will be hardcoded
• If the user is authenticated, he is proposed a menu, inviting him to select among 3 operations (Create, Modify, Delete)

Repeat operations in Java : the while loop

// while
int size = 10;
int i = 0;
while (i < size) {
 //Some repeated instruction
 i++;
}
	

Repeat operations in Java : the do-while loop

// while
int size = 10;
int i = 0;
do{
 //Some repeated instruction
 i++;
} while (i < size);
	

Repeat operations in Java : the for loop

// for-loop
String[] table = new String[10];
for (int i = 0; i < 10; i++) {
	String current = table[i];
	System.out.println(current);
}

// for-loop, "foreach" way
for (String s : table) {
	System.out.println(s);
}
	

Java data structures: Arrays

• Dimension

  //Declares a table of 10 strings
  String[] table = new String[10];
  int tableLength = table.length;
  

• Access by index

  //Accesses the occurrence at the first index
  String occurrence = table[0];
  

Exercise: A factorial implementation

Remember that the factorial is defined by :

• Make a dedicated class named Factorial
• Write three static methods (one for each implementation) and think about the return type
• Write one static void main method calling all the three methods with parameters

Exercise: Completing the project menu